As a sidebar to the recent monetary policy and money creation debate, I have been debating JKH, over at MR, on the nitty gritty details of what the central bank can do to hit new target interbank rates. (We largely agree on the broader issues.) I'm using this post as a venue to lay out my position more clearly, with the aid of graphs. Apologies to those who haven't been following, if this seems like it comes out of nowhere. EDIT: For those who relate to the U.S., we're specifically debating this issue outside of a "floor" system, which is the situation in the U.S. currently. So think something like pre-2008 U.S., as one example. I discuss the issue more generally than the Fed in the U.S., though.
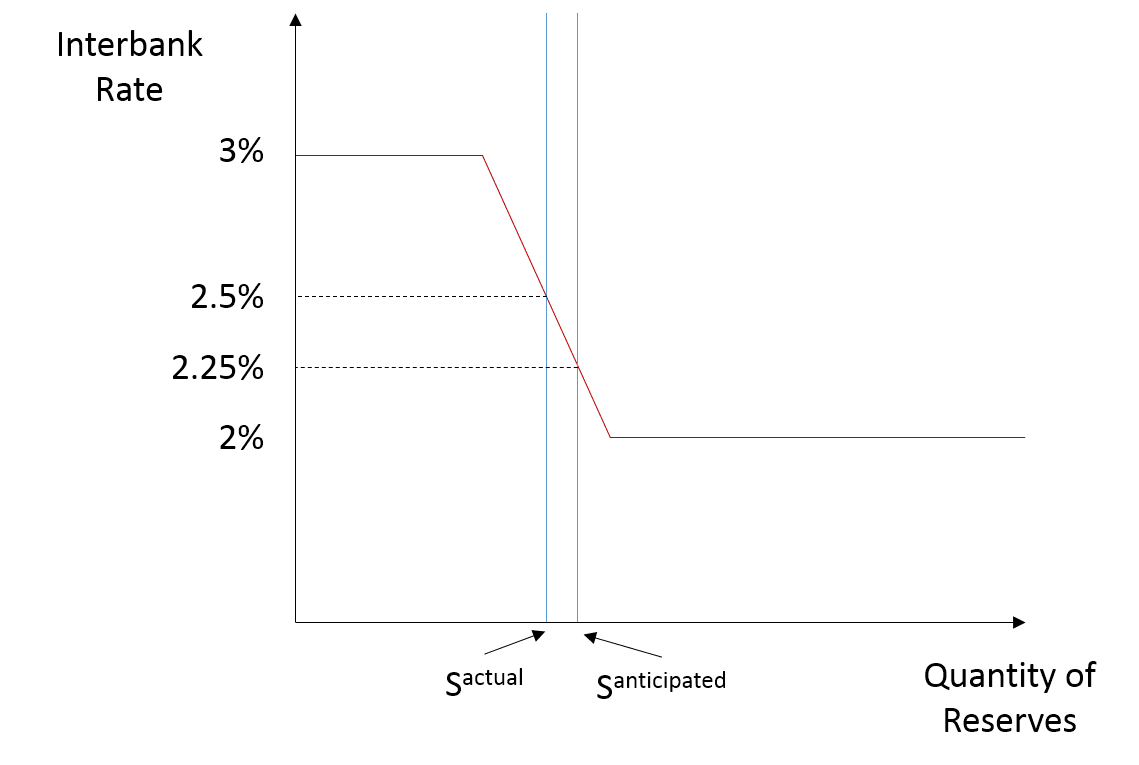
Now suppose that the central bank announces that their new target interbank rate is 2.25%. They announce that they will not be changing the ceiling or floor rates. Holding everything else constant, if the market believes that the central bank will enforce their new target rate, then it must anticipate a movement of the supply curve to the point where a 2.25% market rate would be a profit-maximizing (or cost-minimizing) outcome for the market.
If these are the expectations, the market rate should move to the new target rate prior to the central bank actually shifting the supply curve. However, the market will still expect the central bank to follow through on its implied promise of a shift in the supply curve. If and when the central bank shifts the supply curve, this will not cause the interbank rate to overshoot the target (contrary to my interpretation of JKH's and MMT'ers past assertions).
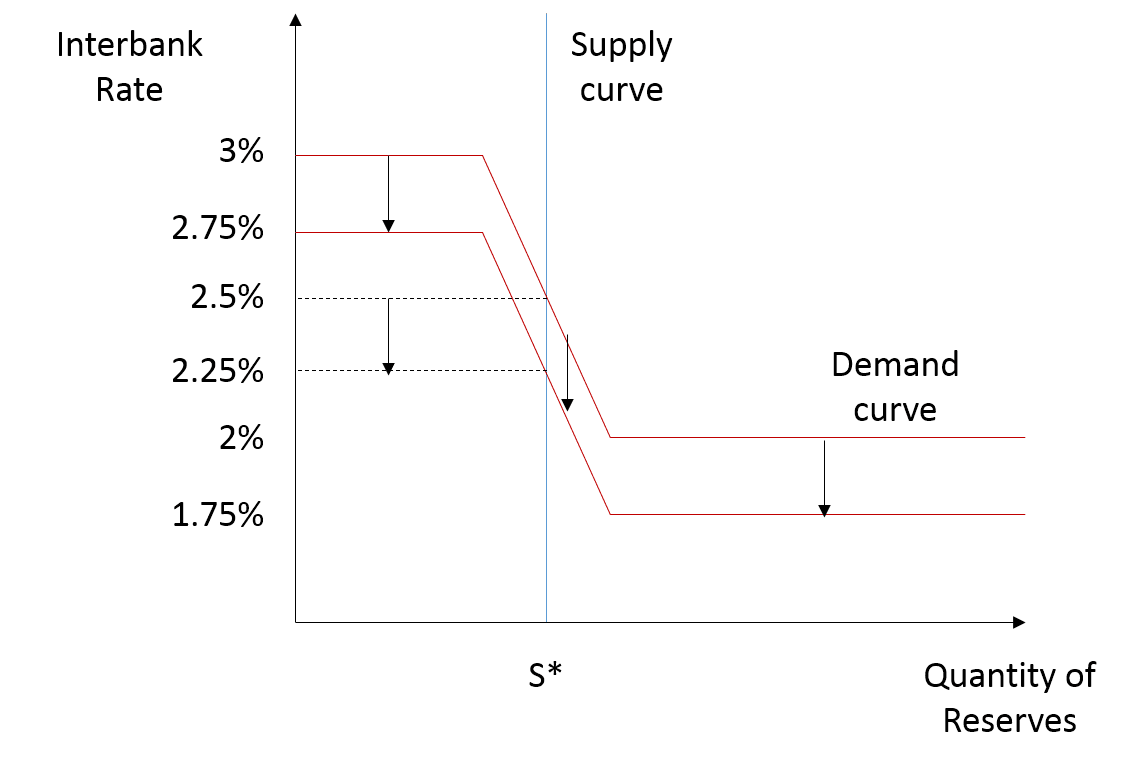
Suppose instead that the central bank announces that their new target interbank rate is 2.25%, but that they will be changing the ceiling and floor rates to 2.75% and 1.75%, respectively. Upon this news, the demand curve should shift downward. In this case, I agree with JKH comments on the automatic shifting of the demand curve. Continuing to assume a 50/50 probability that banks end the reserve maintenance period short or long at the current quantity of reserves S*, then the shifting of the demand curve alone will yield the new target rate, without requiring any change in the quantity of reserves.
In this case, if the central bank were to also inject reserves, then the interbank rate would fall lower than target. The degree to which it would overshoot would depend on how many reserves the central bank injects. But contrary to what I’ve seen in the MMT/MR blogosphere, it would not necessarily fall to the new floor of 1.75%.
As I interpret JKH (and Scott Fullwiler, associated with MMT), altering reserve quantities can only be used to defend a new target rate, not to offensively set a new one.
From their viewpoint, rates move due to an "announcement effect,"
whereby the central bank's announcement of a new target rate is enough to move
the rate without the need for any other action, all else equal. Already, JKH has clarified that he believes the announcement effect must incorporate a change in corridor rates for it to move rates, all else equal. This I agree with, but I don't consider this to be a "pure announcement effect," in which it's only the central bank's words, rather than its actions, that matter. (I'd also add that the movement of the corridor may still not be enough to hit the new target. Depending on the corridor rates and probability of banks ending short or long reserves, quantity changes might be required as well, or more theoretically, a reserve requirement change.)
More generally, my aim is to show them that altering reserve quantities can most certainly be used to offensively achieve a new target rate. Admittedly, I am employing the assumptions that Bindseil and Woodford use in their most basic monetary policy implementation models - but I view these as plenty rigorous for our purposes.
Suppose we start with the following scenario. The central bank’s target rate is 2.5%. The ceiling and floor rates are 3% and 2%, respectively. There is a 50/50 probability that the market will end short or long reserves assuming the quantity of reserves available in the market is exactly equal to the quantity of required reserves. Thus, the central bank sets the quantity of reserves equal to required reserves to achieve their target rate.
FIGURE 1
FIGURE 2
FIGURE 3
In this case, if the central bank were to also inject reserves, then the interbank rate would fall lower than target. The degree to which it would overshoot would depend on how many reserves the central bank injects. But contrary to what I’ve seen in the MMT/MR blogosphere, it would not necessarily fall to the new floor of 1.75%.
In conclusion, if all along, JKH, Fullwiler, et al. had this last case in mind, we would be in agreement. But that was never made clear, in my opinion. Furthermore, the other case, involving a shift in quantity of reserves, is just as fundamentally sound. Understanding both cases allows one to see that monetary policy implementation can be a matter of rates and/or quantity.
APPENDIX A: Changing Reserve Requirements
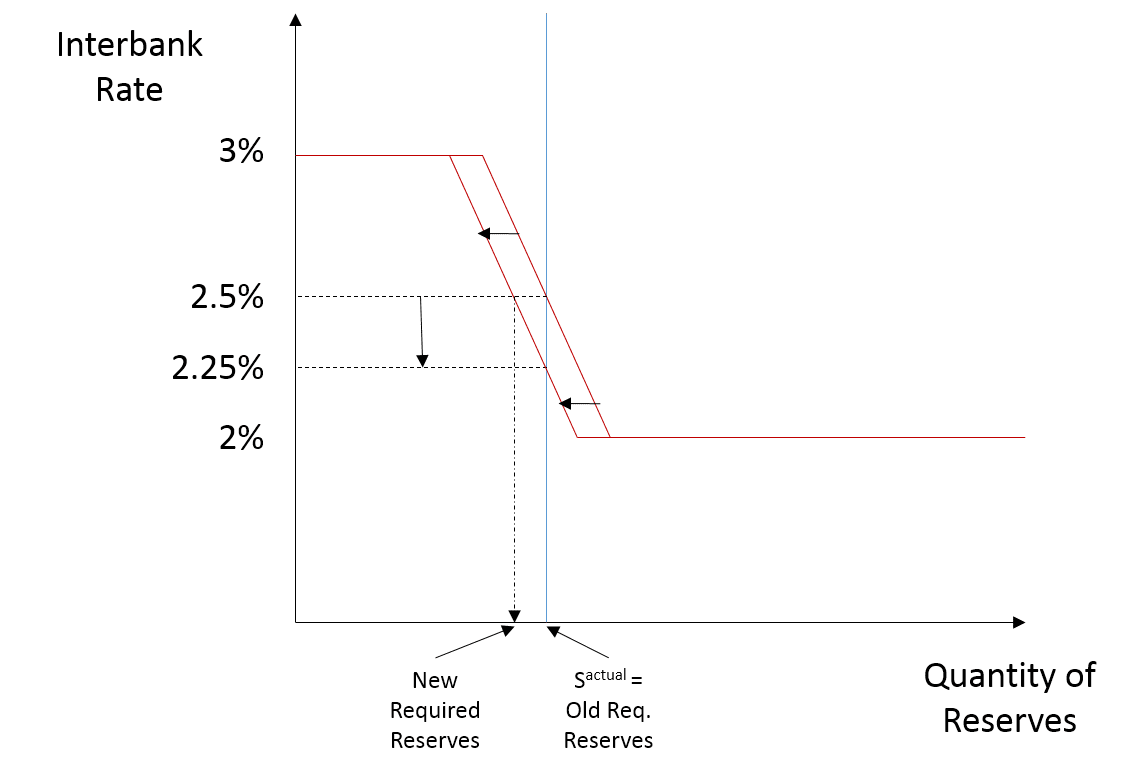
From a previous interbank rate of 2.5%, suppose that the central bank announces that their new target interbank rate is 2.25%. They do not change the ceiling or floors nor the quantity of reserves. Instead, they lower the reserve requirement. This should cause a leftward shift in the demand curve. In other words, given a fixed quantity of reserves, a lower reserve requirement means that banks will be less likely to end the reserve maintenance period short. As such, the interbank rate should drop below 2.5%.
Continuing to assume a symmetric probability distribution (50/50 short/long) around the quantity of required reserves, the central bank could have maintained the 2.5% interest rate if they lowered the actual quantity of reserves to the new quantity of required reserves by conducting an OMO. In our example, the central bank does not do that since they want a lower interbank rate.
APPENDIX B: Interbank Rate Targeting with Fixed Target-Ceiling Spread
Added in from comments: Assume a system similar to the U.S. pre-2008, where there is a fixed spread between the target rate and the ceiling – say it’s 2%. This means that as the target interbank rate changes, its distance from the floor will change, whereas its distance from the ceiling will remain fixed. We might call this an 'asymmetric' channel, in contrast to the 'symmetric' channel of Figure 3 above.
APPENDIX A: Changing Reserve Requirements
From a previous interbank rate of 2.5%, suppose that the central bank announces that their new target interbank rate is 2.25%. They do not change the ceiling or floors nor the quantity of reserves. Instead, they lower the reserve requirement. This should cause a leftward shift in the demand curve. In other words, given a fixed quantity of reserves, a lower reserve requirement means that banks will be less likely to end the reserve maintenance period short. As such, the interbank rate should drop below 2.5%.
FIGURE 4
Continuing to assume a symmetric probability distribution (50/50 short/long) around the quantity of required reserves, the central bank could have maintained the 2.5% interest rate if they lowered the actual quantity of reserves to the new quantity of required reserves by conducting an OMO. In our example, the central bank does not do that since they want a lower interbank rate.
APPENDIX B: Interbank Rate Targeting with Fixed Target-Ceiling Spread
Added in from comments: Assume a system similar to the U.S. pre-2008, where there is a fixed spread between the target rate and the ceiling – say it’s 2%. This means that as the target interbank rate changes, its distance from the floor will change, whereas its distance from the ceiling will remain fixed. We might call this an 'asymmetric' channel, in contrast to the 'symmetric' channel of Figure 3 above.
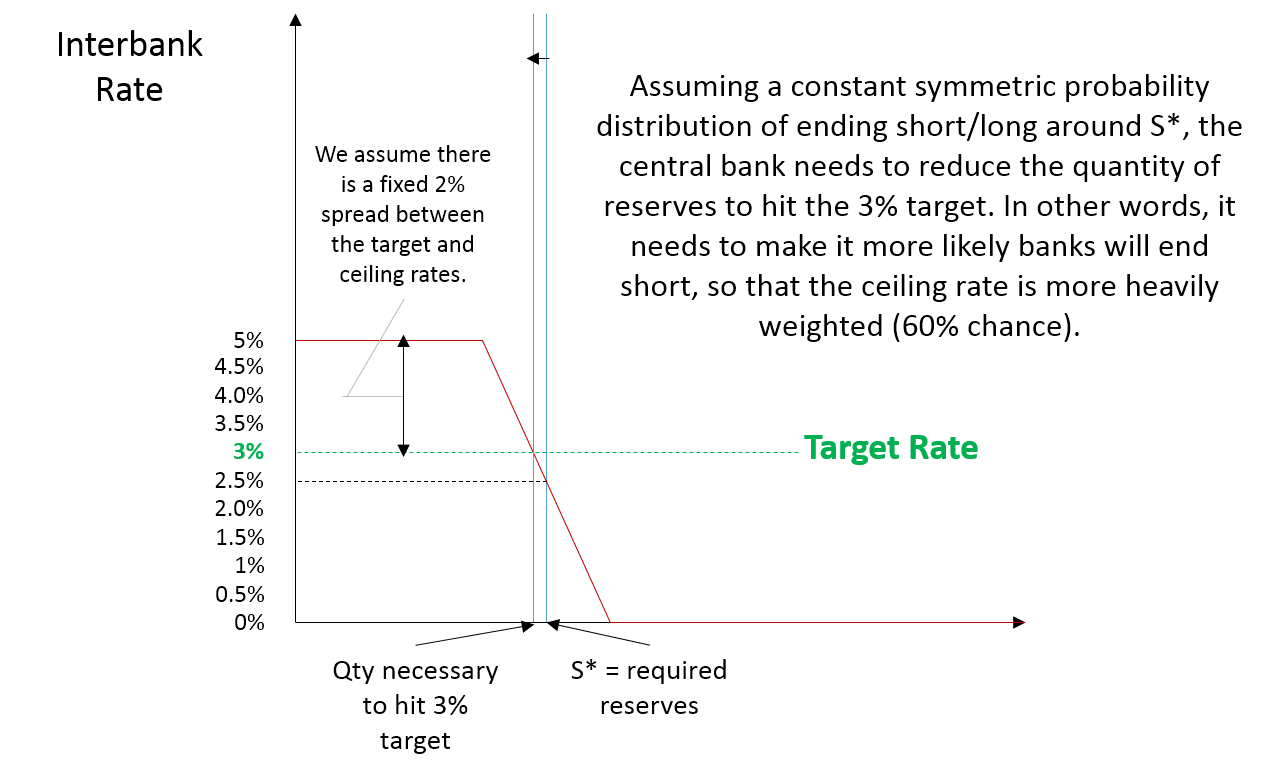
Assume a symmetric probability distribution of anticipated liquidity shocks and, just as a starting point, that the current quantity of reserves in the market is the quantity of required reserves. That means if the target rate is 3%, the ceiling is 5%, and the floor 0%, the interbank rate should be 2.5% (5%*.5 +0%*.5). Therefore the central bank is missing its target. To move the interbank rate up to 3%, the CB is going to have to remove a quantity of reserves so that it becomes more likely the banking system will end the reserve maintenance period short. In particular, there needs to be a 60% chance of this occurring (3% = 5%*.6 + 0%*.4). See Figure 5.
FIGURE 5
Then say the CB changes its target to 2%, which means the ceiling will be 4% (see Figure 6). Now, assuming the same symmetric probability distribution of liquidity shocks, the Fed needs to inject reserves back into the system until the quantity of reserves is the quantity of required reserves (2% = 4%*.5 + 0%*.5). Otherwise, the new rate will be 2.4% (4%*.6 + 0%*.4). In this case, changing the ceiling/floor rates was simply not enough to hit the target. The central bank needed to also change the quantity of reserves, even controlling for any changes in reserve distributions or any other market abnormalities. This is most certainly a liquidity effect. I am not denying that the rate will move to 2% upon announcement, but the central bank still needs to lower the ceiling and reduce the quantity of reserves to maintain the rate as well as its credibility. At least as far as this model goes.
FIGURE 6